2023年曲阜微分方程与动力系统研讨会
一、会议日程安排
7月7日 |
全天 |
注册 |
曲阜市铭座杏坛宾馆 |
7月8日 |
大会报告(地点:杏坛宾馆三楼会议室) |
时间 |
主持人 |
报告人 |
题目 |
8:00-9:00 |
肖冬梅 |
尤建功 |
拟周期薛定谔算子谱理论 |
9:00-10:00 |
李继彬 |
Bifurcations and exact solutions in three optical models: dynamical system approach |
10:00-11:00 |
尤建功 |
韩茂安 |
General study on limit cycle bifurcation near a double homoclinic loop |
11:00-12:00 |
司建国 |
KAM tori for the two-dimensional completely resonant Schrödinger equation with the general nonlinearity |
会场(一) (地点:杏坛宾馆三楼会议室) |
14:00-15:00 |
王培光 |
倪明康 |
具有非法向双曲性的若干奇摄动问题多尺度解 |
15:00-16:00 |
杜增吉 |
Lotka-Volterra competition-diffusion-advection models and predator-prey systems |
16:00-17:00 |
朝 鲁 |
朴大雄 |
Anderson localization for the quasi-periodic CMV matrices with Verblunsky coefficients defined by the skew-shift |
17:00-18:00 |
马如云 |
Global structure of positive solutions for a Neumann problem with indefinite weight |
会场(二) (地点:杏坛宾馆一楼怀德会议室) |
14:00-15:00 |
魏广生 |
綦建刚 |
Measure Sturm-Liouville Eigenvalue Problems and Optimal Recovery Theory |
15:00-16:00 |
储继峰 |
Minimizations of positive periodic and Dirichlet eigenvalues for general indefinite Sturm-Liouville problems |
16:00-17:00 |
高承华 |
周 麒 |
Non-Self-Adjoint Quasi-periodic Operators with complex spectrum |
17:00-18:00 |
李晓迪 |
状态切换系统的稳定性与控制 |
7月9日 |
会场(一) (地点:杏坛宾馆三楼会议室) |
时间 |
主持人 |
报告人 |
题目 |
8:00-9:00 |
额布日力吐 |
张茂柱 |
Regular approximation of some classes of singular differential operators |
9:00-10:00 |
徐小川 |
Stability of the inverse scattering problem for the self-adjoint matrix Schrödinger operator on the half line |
10:00-11:00 |
敖继军 |
柳代权 |
Inverse problems for the Dirac operator on a star graph |
11:00-12:00 |
赵 佳 |
对称度量图上函数空间的正交分解 |
会场(二) (地点:杏坛宾馆一楼怀德会议室) |
8:00-9:00 |
杨传富 |
孙华清 |
On classification of singular matrix difference equations of mixed order |
9:00-10:00 |
周 喆 |
Almost periodic function and rotation number of the Schrödinger operator |
10:00-11:00 |
吴德玉 |
徐新建 |
Inverse spectral problems for radial Schrödinger operators and closed systems |
11:00-12:00 |
刘志文 |
Lyapunov-Type Inequalities and Extremal Estimates of Nonlocal Sturm-Liouville Eigenvalue Problems |
会场(一) (地点:杏坛宾馆三楼会议室) |
14:00-15:00 |
孙华清 |
关爱薇 |
Solving Barcilon’s inverse problems by the method of spectral mappings |
|
15:00-16:00 |
吕 康 |
One dimensional discrete Schrödinger operators with resonant embedded eigenvalues |
|
16:00-17:00 |
傅守忠 |
青 兰 |
对称微分算子的Friedrichs 扩张 |
|
17:00-18:00 |
赵 敏 |
Optimal inverse problems of potentials for two given eigenvalues of Sturm-Liouville problems |
|
会场(二) (地点:杏坛宾馆一楼怀德会议室) |
14:00-15:00 |
郑召文 |
敖继军 |
Eigenvalue properties of third-order boundary value problems with distributional potentials |
|
15:00-16:00 |
胡怡腾 |
Inverse spectral problem for differential pencils with a frozen argument |
|
16:00-17:00 |
白占兵 |
王 丰 |
Traces and a partial inverse problem for Sturm-Liouville operators with constant delays on a star graph |
|
17:00-18:00 |
杨 璐 |
Inverse problems for a damped Stieltjes string with mixed spectral data |
|
二、学术报告题目与摘要
大会报告
报告题目:拟周期薛定谔算子谱理论
报 告 人:尤建功 教授 南开大学
报告摘要:本报告简要介绍拟周期薛定谔算子的背景、问题和进展。
报告题目:Bifurcations and exact solutions in three optical models: dynamical system approach
报 告 人:李继彬 教授 浙江师范大学
报告摘要:For three optical models, this talk introduces how to use the theory of dynamical systems and study method of singular traveling wave system developed by [Li & Chen, 2007] to find exact solutions and understand the existence of peakons, periodic peakons, pseudo-peakon and compactons in these models.
报告题目:General study on limit cycle bifurcation near a double homoclinic loop
报 告 人:韩茂安 教授 浙江师范大学
报告摘要:In this paper, we study the bifurcation problem of limit cycles near a general double homoclinic loop. We establish a general theory to obtain a sharp lower bound of the maximal number of limit cycles near the double homoclinic loop. As an application, we prove that a Li\'{e}nard system of the form \dot{x}=y(y^2-1)+\varepsilon \sum\limits_{i=0}^na_ix^{2i+1}, \dot{y}=-x has at least $[\frac{5}{2}n]$ limit cycles. This number is maximal that we can find so far for the system.
报告题目:KAM tori for the two-dimensional completely resonant Schrödinger equation with the general nonlinearity
报 告 人:司建国 教授 山东大学
报告摘要:In this talk, two-dimensional completely resonant Schrödinger equation with the general nonlinearity under periodic boundary conditions is considered. For any given positive integers p and b, it is obtained that a Whitney smooth family of small-amplitude b-quasi-periodic solutions for the equation by developing an abstract KAM (Kolmogorov-Arnold-Moser) theorem for infinite dimensional Hamiltonian systems.
邀请报告
报告题目:具有非法向双曲性的若干奇摄动问题多尺度解
报 告 人:倪明康 教授 华东师范大学
报告摘要:针对系统退化流形具有非法向双曲性的若干右端不连续奇摄动微分方程边值问题,作者将利用奇摄动方法中的空间对照结构理论并结合几何奇摄动理论中的“吹胀法”和交换引理,不但证明各类边值问题光滑解的存在性,而且构造一致有效光滑解,并给出了误差估计。具体介绍了二阶奇摄动半线性边值问题当退化方程具有重根时所出现的各种复杂的动力学现象。
报告题目:Lotka-Volterra competition-diffusion-advection models and predator-prey systems
报 告 人:杜增吉 教授 江苏师范大学
报告摘要:In this talk, we mainly investigate Lotka-Volterra competition-diffusion -advection systems and predator-prey systems with Holling type functional response. By employing the Lyapunov-Schmidt reduction method, we obtain the existence of steady state solution. We obtain the stability and Hopf bifurcation at the spatially nonhomogeneous steady-state by means of by the center manifold reduction and the normal form theory. By using the geometric singular perturbation theory and constructing a locally invariant manifold, we prove the existence of the traveling wave solutions to predator-prey systems.
报告题目:Anderson localization for the quasi-periodic CMV matrices with Verblunsky coefficients defined by the skew-shift
报 告 人:朴大雄 教授 中国海洋大学
报告摘要:We study quasi-periodic CMV matrices with Verblunsky coefficients given by the skew-shift. We prove the positivity of Lyapunov exponents and Anderson localization for most frequencies, which establish the analogous results of one-dimensional Schrödinger operators proved by Bourgain, Goldstein and Schlag (Commun. Math. Phys,2001)。
Joint work with Shuzheng Guo and Yanxue Lin.
报告题目:Global structure of positive solutions for a Neumann problem with indefinite weight
报 告 人:马如云 教授 西安电子科技大学
报告摘要:We show that the global structure of positive solutions for the Neumann problem involving mean curvature operator
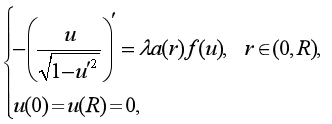
Where  is a parameter,
is a parameter,  is an
is an  -function which is allowed to change sign and
-function which is allowed to change sign and  is continuous. Depending in the behavior of
is continuous. Depending in the behavior of  near 0 and
near 0 and  , we obtain that there exists
, we obtain that there exists  such that for any
such that for any  , problem (P) possesses at least two solutions , while it has no solution for
, problem (P) possesses at least two solutions , while it has no solution for  . The proof of the main results is based upon bifurcation method.
. The proof of the main results is based upon bifurcation method.
报告题目:Measure Sturm-Liouville Eigenvalue Problems and Optimal Recovery Theory
报 告 人:綦建刚 教授 山东大学(威海)
报告摘要:In this report,we introduce the latest progress of differential equations for Measure Sturm-Liouville Eigenvalue Problems and Optimal Recovery Theory.
报告题目:Minimizations of positive periodic and Dirichlet eigenvalues for general indefinite Sturm-Liouville problems
报 告 人:储继峰 教授 上海师范大学
报告摘要:This talk will focus on the sharp estimates for eigenvalues of a general Sturm-Liouville problem , where
, where  is a nonnegative potential and another potential
is a nonnegative potential and another potential admits to change sign. A typical example of such problems is the well-known Camassa-Holm equations with indefinite potentials. We will show that the solution of the minimization problems of eigenvalues will lead to more general distributions of potentials which have no densities with respect to the Lebesgue measure, and it is very natural to choose the general setting of the measure differential equations to understand the eigenvalues and their minimization.
admits to change sign. A typical example of such problems is the well-known Camassa-Holm equations with indefinite potentials. We will show that the solution of the minimization problems of eigenvalues will lead to more general distributions of potentials which have no densities with respect to the Lebesgue measure, and it is very natural to choose the general setting of the measure differential equations to understand the eigenvalues and their minimization.
报告题目:Non-Self-Adjoint Quasi-periodic Operators with complex spectrum
报 告 人:周麒 教授 南开大学陈省身数学所
报告摘要:We give a precise and complete description on the spectrum for a class of non-self-adjoint quasi-periodic operators acting on $\ell^2(\mathbb{Z}^d)$ which contains the Sarnak's model as a special case. As a consequence, one can see various interesting spectral phenomena including $\mathscr{P}\mathscr{T}$ symmetric breaking, the non-simply-connected two-dimensional spectrum in this class of operators. Particularly, we provide new examples showing that the spectrum of the limit operator in $\ell^2(\mathbb{Z})$ (actually a two-dimensional set in $\mathbb{C}$) can not be approximated by the spectra of the finite-intervals operators.
报告题目:状态切换系统的稳定性与控制
报 告 人:李晓迪 教授 山东师范大学
报告摘要:报告主要介绍状态切换系统稳定性与控制方面研究进展。首先,简要介绍一下研究团队近年的研究工作。然后,根据切换机理的不同,分别介绍时间切换和状态切换的研究现状和研究热点,重点介绍团队在切换延迟系统的跟踪控制,切换随机神经网络的稳定性等方面的最新成果。最后介绍团队下一步拟开展的研究工作。
报告题目:Regular approximation of some classes of singular differential operators
报 告 人:张茂柱 副教授 泰山学院
报告摘要:Given a regular Sturm-Liouville problem with self-adjoint boundary conditions, it has only point spectrum, i.e. eigenvalues of the problem. The numerical computation of eigenvalues is widely studied by many authors, such as the codes SLEIGN2 and SLEUTH constructed by Baily, Shampine, Greenberg and Marletta. These codes can deal with singular problems as well as regular ones and the fundamental idea is to truncate the interval near a singular endpoint. The fundamental theory is to approximate the spectra of singular problems with the eigenvalues of regular problems, i.e. regular approximation of singular differential operators. In this report, we will discuss regular approximation of three classes of singular differential operators: (1) Singular SL problems with eigenparameter-dependent boundary conditions; (2) Singular Hamiltonian systems with two singular endpoints; (3) The third-order differential operators.
报告题目: Stability of the inverse scattering problem for the self-adjoint matrix Schrödinger operator on the half line
报 告 人: 徐小川 副教授 南京信息工程大学
报告摘要: In this report, we introduce the stability results on the inverse scattering problem for the self-adjoint matrix Schrödinger operator on the half line. We estimate the difference of two potentials and the difference of the two unitary matrices in the boundary conditions when the two sets of scattering data are close enough (or coincide) on a finite interval.
报告题目: Inverse problems for the Dirac operator on a star graph
报 告 人: 柳代权 讲师 扬州大学
报告摘要: Following the previous work, we shall study some inverse problems for the Dirac operator on an equilateral star graph. It is proven that the so-called Weyl function uniquely determines the potentials. Furthermore, we pay attention to the inverse problem of recovering the potentials from the spectral data, which consists of the eigenvalues and weight matrices, and present a constructive algorithm. The basic tool in this paper is the method of spectral mappings developed by Yurko.
报告题目: 对称度量图上函数空间的正交分解
报 告 人: 赵佳 副教授 河北工业大学
报告摘要: 度量图上微分算子(量子图)作为研究复杂的网络或介观结构中粒子行为的数学模型,其自伴性与谱性质依赖度量图的拓扑结构与几何特征,其中,一些具有对称性的量子图具有独特的谱结构(能带结构)。本报告分析径向度量图和具有~$\frac{2\pi}{n}$~旋转不变性的度量图上平方可积函数空间,通过群表示的相关理论, 得到函数空间的正交分解及对应量子图的商图,将原量子图的谱问题简化,给出久期行列式的对应分解。为后续具有对称性的量子图谱性质的研究奠定有力基础。
报告题目:On classification of singular matrix difference equations of mixed order
报 告 人:孙华清 教授 东北大学
报告摘要:This talk is concerned with singular matrix difference equations of mixed order. The existence and uniqueness of initial value problems for these equations are derived, and then the classification of them is obtained with a similar classical Weyl’s method by selecting a suitable quasi-difference. An equivalent characterization of this classification is given in terms of the number of linearly independent square summable solutions of the equation. The influence of off-diagonal coefficients on the classification is illustrated by two examples. In particular, two limit point criteria are established in terms of coefficients of the equation.
报告题目: Almost periodic function and rotation number of the Schrödinger operator
报 告 人: 周喆 副研究员 中国科学院数学与系统科学研究院
报告摘要: The concept of almost periodic functions is due to H. Bohr. The concept of rotation number is due to H. Poincaré. The Schrödinger operator is named after E. Schrödinger. I will present our work related with these issues. (with David Damanik and Meirong Zhang).
报告题目: Inverse spectral problems for radial Schrödinger operators and closed systems
报 告 人: 徐新建 博士后 南京理工大学
报告摘要: We study an inverse eigenvalue problem for the radial Schrödinger operators on the unit interval. This problem consists in the recovery of the potential on a subinterval (0, a), a≤1, from eigenvalues corresponding to the boundary value problems with different boundary conditions. We obtain a sufficient condition for the unique specification of the radial Schrödinger operator by a set of eigenvalues and a part of the potential function on (a, 1) in terms of the cosine system closedness. The Borg-type and the Hochstadt-Lieberman type results are obtained as corollaries of our main result. Furthermore, under an additional hypothetical condition, we show that our condition is not only sufficient but also necessary for the uniqueness of the inverse problem solution. The main tool of our proof technique is the singular transformation operator representation for the solution of the radial Schrödinger equation.
报告题目: Lyapunov-Type Inequalities and Extremal Estimates of Nonlocal Sturm-Liouville Eigenvalue Problems
报 告 人: 刘志文 博士生 山东大学(威海)
报告摘要: Lyapunov-type inequalities are given for nonlocal Sturm-Liouville boundary value problems. With applications, we investigate the extremal problems of L1-norm for " local" potentials of Sturm-Liouville eigenvalue problems with "nonlocal" terms if the first eigenvalue is known.
报告题目: Solving Barcilon’s inverse problems by the method of spectral mappings
报 告 人: 关爱薇 博士生 南京理工大学
报告摘要: In this paper, we consider Barcilon’s inverse problem, which consists of the recovery of the fourth-order differential operator from three spectra. We obtain the relationship of Barcilon’s three spectra with the Weyl-Yurko matrix. Moreover, we prove the uniqueness theorem for the inverse problem solution by developing the ideas of the method of spectral mappings. Our approach allows us to obtain the result for the general case of complex-valued distributional coefficients. In the future, the methods and the results of this paper can be generalized to differential operators of orders greater than 4 and used for further development of the inverse problem theory for higher-order differential operators.
报告题目: One dimensional discrete Schrödinger operators with resonant embedded eigenvalues
报 告 人: 吕康 博士生 南京理工大学
报告摘要: In this paper, we introduce a new family of functions to construct Schrödinger operators with embedded eigenvalues. This allows us to construct discrete Schrödinger operators with arbitrary prescribed sets of eigenvalues.目: Eigenvalues of Sturm-Liouville problems with eigenparameter dependent boundary and interface conditions.
报告题目: 对称微分算子的Friedrichs 扩张
报 告 人: 青兰 助理研究员 陕西师范大学
报告摘要: 半有界对称微分算子理论在微分算子谱理论的研究中具有十分重要的作用。对于下半有界对称微分子,我们得到了其Friedrichs扩张的描述,更加显性地刻画了Friedrichs扩张的边界条件,进一步发展和完善了Friedrichs扩张问题的结论。
报告题目: Optimal inverse problems of potentials for two given eigenvalues of Sturm-Liouville problems
报 告 人: 赵敏 硕士生 山东大学(威海)
报告摘要: The infmum of the norm of potentials is given for Sturm-Liouville eigenvalue problems with Dirichelet boundary condition such that the first two eigenvalues are known. The explicit quantity of the infimum is given by the two eigenvalues.
报告题目:Eigenvalue properties of third-order boundary value problems with distributional potentials
报 告 人:敖继军 教授 内蒙古工业大学
报告摘要:In this talk, we discuss several eigenvalue properties of the third-order boundary value problems with distributional potentials. Firstly, we prove that the operators associated with the problems are self-adjoint and the corresponding eigenvalues are real. Next, the continuity and differential property of the eigenvalues of the problems are given, especially we find the differential expressions for the boundary conditions, the coefficient functions and the endpoints. Finally, we show a brief application to a kind of transmission boundary value problems of the problems studied here.
报告题目: Inverse spectral problem for differential pencils with a frozen argument
报 告 人: 胡怡腾 讲师 西安电子科技大学
报告摘要: This paper deals with differential pencils possessing a term depending on the unknown function with a fixed argument. We deduce the so-called main equation together with its fine structure for the spectral problem. Then, according to the boundary conditions and the position of argument, we describe two cases: degenerate and non-degenerate. For these two cases, the uniqueness of inverse spectral problem is studied and a constructive procedure for reconstructing the potentials along with necessary and sufficient conditions of the inverse problem solvability are obtained.
报告题目: Inverse problems for a damped Stieltjes string with mixed spectral data
报 告 人: 王丰 讲师 南京理工大学
报告摘要: In this talk, we consider the Sturm-Liouville operators with constant delays on a star graph. First, the asymptotics for the large eigenvalues of these operators are obtained. Secondly, the regularized trace formulae of these operators are established with the method of complex analysis. Finally, we state a partial inverse problem for the Sturm-Liouville operators with constant delays on a star graph, and provide the uniqueness theorem as well as a constructive method for the solution of the inverse problem.
报告题目: Inverse problems for a damped Stieltjes string with mixed spectral data
报 告 人: 杨璐 讲师 西安电子科技大学
报告摘要: In this report, we are concerned with inverse problems for Stieltjes strings with damping at the end or at an interior point. We take Krein-Nudelman interpolation as the main tool, and we solve inverse problems for Stieltjes strings of uniquely recovering parameters of the strings using partial information on the strings and partial information on the spectrum.
 首页
>
正文
首页
>
正文
 首页
>
正文
首页
>
正文